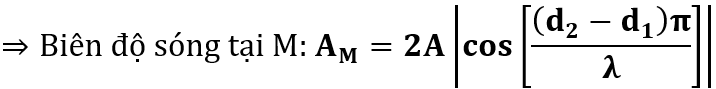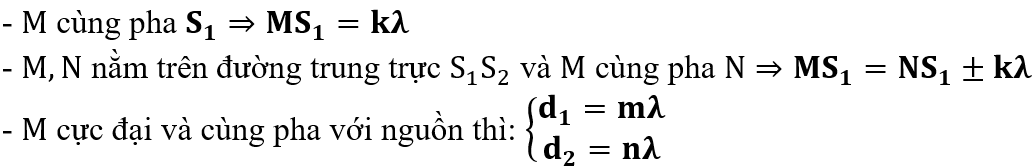CHỦ ĐỀ 3. GIAO THOA SÓNG
I. ĐIỀU KIỆN ĐỂ CÓ GIAO THOA
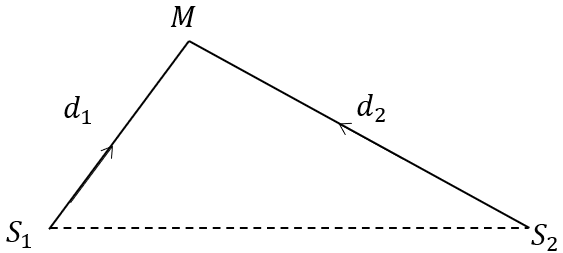
Muốn có giao thoa hai nguồn phải là hai nguồn kết hợp.
Hai nguồn kết hợp là hai nguồn dao động CÙNG tần số, cùng phương và có độ lệch pha không đổi theo thời gian.
II. GIAO THOA HAI NGUỒN CÙNG BIÊN ĐỘ
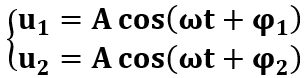
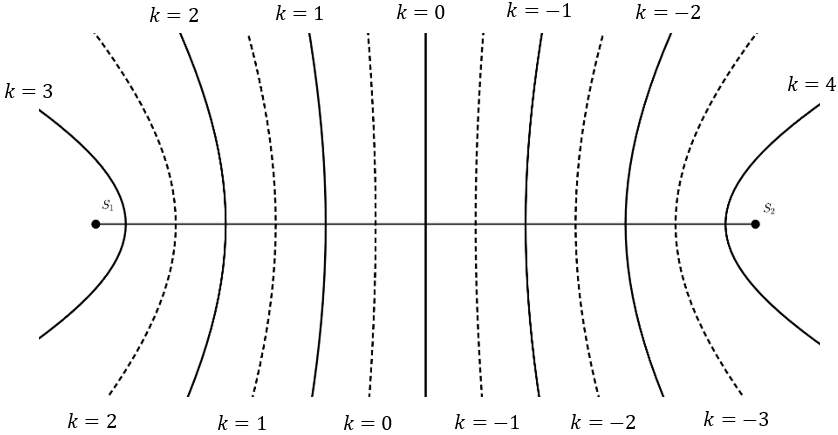
1. HAI NGUỒN CÙNG PHA
| CỰC ĐẠI |
Vân trung tâm là vân cực đại (biên độ 2A)
|
|
| CỰC TIỂU | ||
| SỐ ĐIỂM CỰC ĐẠI TRÊN S1S2 | ||
| SỐ ĐIỂM CỰC TIỂU TRÊN S1S2 | ||
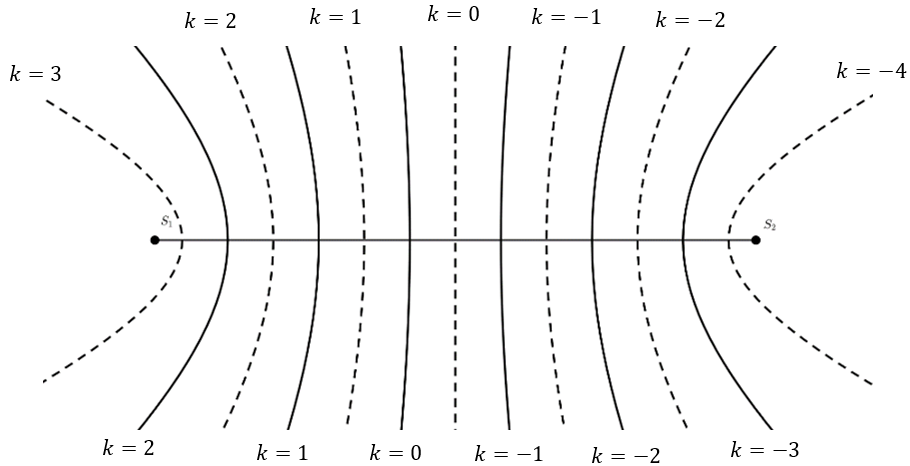
2. HAI NGUỒN NGƯỢC PHA
| CỰC ĐẠI |
Vân trung tâm là vân cực tiểu (đứng yên có biên độ bằng 0)
|
|
| CỰC TIỂU | ||
| SỐ ĐIỂM CỰC ĐẠI TRÊN S1S2 | ||
| SỐ ĐIỂM CỰC TIỂU TRÊN S1S2 | ||
3. HAI NGUỒN VUÔNG PHA
|
Vân trung tâm có biên độ A√2 |
|
| CỰC ĐẠI | |
| CỰC TIỂU | |
| SỐ ĐIỂM CỰC ĐẠI TRÊN S1S2 | |
| SỐ ĐIỂM CỰC TIỂU TRÊN S1S2 | |
4. HAI NGUỒN LỆCH PHA
| CỰC ĐẠI | |
| CỰC TIỂU | |
III. SỐ ĐIỂM CỰC ĐẠI - CỰC TIỂU TRÊN M,N
1. M, N CÙNG MỘT BÊN
Xét M (d1, d2) => k1
Xét M (d1’, d2’) => k2
=> Số điểm cực đại (cực tiểu) trên đoạn MN là: k1 ≤ k ≤ k2
2. M, N NẰM HAI BÊN
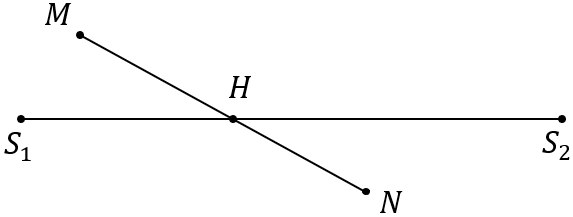
Số điểm cực đại (cực tiểu) trên đoạn MN = Số điểm trên MH + Số điểm trên HN.
IV. SỐ ĐIỂM CỰC ĐẠI TRÊN ĐƯỜNG TRÒN (elip)

LƯU Ý
- Khoảng cách giữa hai cực đại liên tiếp hoặc hai cực tiểu liên tiếp nằm trên S1S2 là λ/2
- Các đường cực đại, cực tiểu ứng với k ≥ 0 luôn nằm bên trái vân trung tâm
- Số đường cực đại, cực tiểu quan sát được bằng số điểm cực đại, cực tiểu trên S1S2
- Nếu hai nguồn CÙNG BIÊN ĐỘ thì cực đại có biên độ 2A , cực tiểu có biên độ 0 (đứng yên)
- Nếu hai nguồn KHÁC BIÊN ĐỘ thì:
Cực đại có biên độ bằng A1 + A2.
Cực tiểu có biên độ bằng |A1 – A2| (lúc này cực tiểu KHÔNG đứng yên)
* Cho hai nguồn cùng biên độ.
Phương trình sóng tại M: ![]()